Bond yield by linear interpolation. Bond yields: in simple terms. Coupon yield is investor's interest
1.8. The internal yield of a bond.
The term structure of interest rates.
We will study the analysis of financial investments under certainty conditions using the example of fixed income securities. The most common type of such securities are bonds.
Bond It is an obligation to pay, at certain points in the future, predetermined sums of money. The main parameters of the bond are the nominal price (face value), the maturity date, the size and terms of payments on the bond. From the moment of issue to maturity, bonds are bought and sold on the stock market. The market price of a bond is set on the basis of supply and demand and may be equal to its face value, above or below face value.
We will consider bonds under conditions of certainty: the issuer cannot call the bond before the set maturity date, the payments on the bond are set by fixed values at certain points in time. At the same time, the receipt of future income exactly on time and in full is considered guaranteed. Such bonds are said to have no credit risk. The main risk factor remains interest rate risk – the risk of changes in market interest rates.
Consider a bond for which t 1 , t 2 ,…, t n years from the current time t= 0, where 0< t 1 < t 2 <…< t n , promise to pay sums of money With 1 , With 2 ,…, With n respectively. It's obvious that C i > 0, i = 1, 2,…, n. Let be P is the market value of the bond at the time t= 0. Then it is natural to assume that P < With 1 + With 2 +…+ With n. Moment of time t= 0 - this is the moment at which it is supposed to invest in the bond or the moment of buying the bond. Moment of time t= t n, when the last payment on the bond is made, is called the moment of redemption of the bond, and the period T = t n(in years) – maturity date. Two indicators are mainly of interest to the investor - the yield and the price of the bond. Internal return is the most important and most widely used measure of bond valuation. Also known as yield to maturity.
Definition. Annual internal return bonds r is the annual rate compound interest, according to which the present value of the bond payment stream is equal to the market value of the bond at the moment t= 0:
Here, the internal yield of a bond is defined as the annual return on cash flow With 1 , With 2 ,…,With n, the cost of which P(see paragraph 1.4).
In foreign practice, there is a market agreement according to which if payments on a bond are paid at regular intervals m once a year, the annual nominal rate internal return j :
 .
.
Properties of the internal yield of a bond.
1. The internal rate of return of a bond is equal to the prevailing market interest rate for investments in alternative financial instruments with the same degree of risk. In other words, the rate of internal return of a bond is equal to the yield of comparable instruments.
2. The annual internal yield of a bond is the rate of return that an investor receives if two conditions are met:
1) the investor owns the bond until it is redeemed t= t n ;
2) all payments on the bond are reinvested at a rate equal to the internal yield of the bond r at the time of its purchase.
Let us show that under these conditions, the average annual return on an investment in a bond is equal to its internal return. The purchase of a bond, then holding it until maturity with reinvestment of incoming income will be considered as a financial transaction (see paragraph 1.2). Operation term T
= t n years. Monetary value of the beginning of the operation P(0) is market price bond purchases P in the moment t= 0. According to (8.1), P
=
 . Monetary value of the bond maturity date t= t n for an investor under conditions 1), 2) is the amount P(t n)
=
. Monetary value of the bond maturity date t= t n for an investor under conditions 1), 2) is the amount P(t n)
=
 . According to the definition of profitability of a financial transaction (2.2):
. According to the definition of profitability of a financial transaction (2.2):
P(t n)
= P ,
,
where  - the average annual return on investment in a bond for a period T
= t n years. Let us substitute into this equality the expressions for P and P(t n):
- the average annual return on investment in a bond for a period T
= t n years. Let us substitute into this equality the expressions for P and P(t n):
 =
=

 .
.
Where do we get r
=
 .
.
Thus, the average annual return on investment in a bond, equal to r, is realized on the day of bond redemption if conditions 1), 2) are met. Hence, another name for internal return is yield to maturity. If items 1) or 2) are not met, then the real return received by the investor may be higher or lower than the internal return of the bond. The risk an investor faces when buying a bond is the risk that future reinvestment rates will be below the internal rate of return. This risk is called reinvestment risk or reinvestment rate risk.
The internal yield of a bond is used to evaluate the attractiveness of alternative investment vehicles. Ceteris paribus, the higher the yield to maturity of the bonds of a given issue, the more attractive it is.
Consider the problem of determining the internal yield of a bond. The internal yield of a bond is the solution to equation (8.1). According to Theorem 4.1, this equation under the condition P < With 1 + With 2 +…+ With n has a unique positive solution. This solution is found using approximate methods. One of them is the linear interpolation method (described in paragraph 1.4, examples 4.2, 4.4).
Example 8.1. Determine the annual internal return r bonds, the payment stream for which is indicated in the table:
The approximate value of the internal yield of the bond will be found by the method of linear interpolation. According to the definition of the annual internal return of a bond
 .
.
It is necessary to find a solution to the equation F(r) = 0, where
F(r)
=
 .
.
Since 948<
50 + 1050, то
согласно теореме 4.1 существует единственное
положительное решение этого уравнения.
Так как F(0,07)
= –
15,8396,
F(0.08) = 1.4979, then the desired internal return r
 (0.07; 0.08). By formula (4.8) we find the first approximation
(0.07; 0.08). By formula (4.8) we find the first approximation
r l1 = 0.07 + .
In this case, the value of the function F(r k1) = 0.02567 > 0. Hence, the solution r
 (0.07; 0.07914). The next step of the method gives
(0.07; 0.07914). The next step of the method gives
r l2 = 0.07 + .
Therefore, it can be considered that r
 0.07913 or 7.913% to three decimal places.
0.07913 or 7.913% to three decimal places.
Definition. A bond is called a pure discount bond if only one payment is made on that bond.
Definition. The intrinsic yield of a purely discount bond with no credit risk that has a maturity of t years is called the annual risk-free interest rate for investment in t years. Another name is annual spot rate.
Let be BUT is the redemption amount of a pure discount bond, t years - maturity date, R is the market price of the bond at the moment t = 0, r(t) is the internal yield of the bond. Then, according to the definition of the internal yield of a bond,
 .
.
 (8.2)
(8.2)
is the annual risk-free interest rate for investments in t years.
An example of a purely discount bond with no credit risk is US Treasury zero coupon bonds. Treasury yields serve as a benchmark for all types of bonds.
Consider how any bond can be valued if there are pure discount bonds in the market. Suppose there is a bond in the market AT without credit risk, for which through t 1 , t 2 ,…, t n years promise to pay sums of money With 1 , With 2 ,…, With n respectively. bond AT can be estimated if we consider it as a portfolio of purely discount bonds AT 1 , AT 2 ,…, AT n with maturities in t 1 , t 2 ,…, t n years respectively. Let's assume the following conditions are met:
1) annual risk-free interest rates are known r(t 1), r(t 2), …, r(t n) for investments on t 1 , t 2 ,…, t n years counted from the moment t = 0;
2) pure discount bonds AT 1 , AT 2 ,…, AT n can be purchased on the market in any quantity without transaction costs. Then for these bonds we have
 ,
,
i
= 1, 2, …, n, where P i– current market price of one bond i- of the first kind, A i- the amount to be redeemed on this bond, r(t i) is its internal return. Payment With 1 of the portfolio is redeemed in bonds AT 1 , payment With 2 - bonds AT 2 , etc., payment With n- bonds AT n. Then in the portfolio  ,
i
= 1, 2, …, n, bonds of each type. Therefore, the value of the portfolio at the moment t= 0 is
,
i
= 1, 2, …, n, bonds of each type. Therefore, the value of the portfolio at the moment t= 0 is
 .
.
Then the market value of the bond AT in the moment t= 0 is
 .
(8.3)
.
(8.3)
Each bond payment AT discounted individually at the appropriate risk-free interest rate.
Definition. A set of annual risk-free interest rates r(t 1),
r(t 2),
…, r(t n) for investments on t 1
, t 2 ,…,
t n years counted from the moment t= 0, where  , is called the term structure of interest rates.
, is called the term structure of interest rates.
Thus, if the term structure of interest rates is known, then the cost of a bond that does not have credit risk can be calculated using formula (8.3).
Definition. Function Graph r = r(t), where r(t) is the annual risk-free interest rate for investments in t years is called the yield curve (or spot rate curve).
In real market conditions, there is always only a finite set of purely discount bonds (for example, there are no zero-coupon US Treasury bonds maturing more than one year). Therefore, the yield curve cannot be built only from observations in the market. In this regard, a theoretical yield curve is constructed. To do this, using the yield of real-life purely discount bonds, calculate the theoretical values of yield for various investment periods. There are several methods for obtaining theoretical returns. One of them is called the bootstrap procedure. Let's look at this method with an example.
Example 8.2. There are government bonds A, B, C, D, E on the market, the payment flows for which and the prices at the moment t= 0 are specified in the table:
|
Term in years |
||||||
A and B are purely discount bonds. Their internal returns r(0.5) = 5.25% and r(1) = 6.3%, determined by formula (8.2), are risk-free interest rates for investments for 0.5 years and 1 year. Knowing these two rates, we can calculate the theoretical risk-free interest rate for investments for 1.5 years, using bond C. The price of bond C according to the formula (8.3) is equal to
118,71 =
 ,
,
where r(0,5) = 0,0525, r(1) = 0.063. Then
118,71 =
 .
.
Where do we get the theoretical annual risk-free interest rate for investments for 1.5 years: r(1.5) = 6.9%. This rate is the rate that the market would offer on 1.5-year net discount bonds if such securities actually existed.
Knowing the theoretical 1.5-year risk-free interest rate, you can calculate the theoretical two-year risk-free interest rate using bond D:
Where r(2) = 7.1% is the theoretical two-year risk-free interest rate. Applying once again the described procedure for bond E, we determine the theoretical 2.5-year risk-free interest rate: r(2,5) = 7,9 %.
Risk free interest rates r(0,5), r(1), r(1,5), r(2), r(2.5), built using such a process, set the time structure of interest rates for a 2.5-year range relative to the time point to which bond prices refer.
Knowing the term structure of interest rates r(t 1), r(t 2), …, r(t n), it is possible to construct a yield curve. One of the methods for constructing a curve is linear interpolation. Believe
 ,
,
 ,
i
= 1, 2, …, n
– 1. (8.4)
,
i
= 1, 2, …, n
– 1. (8.4)
To  The yield curve for the term structure obtained in Example 8.2, using linear interpolation, is:
The yield curve for the term structure obtained in Example 8.2, using linear interpolation, is:
Using the yield curve, you can determine the approximate value of the risk-free interest rate for investments for any period from t 1 to t n years. For example, since 1.25  , then
, then
r(1,25)
 r(1)
r(1)
 = 0,066.
= 0,066.
Another way to plot the yield curve is interpolation ( n- 1) - th order:
r(t)


+
 (8.5)
(8.5)
…………………..
+
 ,
,
where t [t 1 ,
t n]. Then r(t) is a polynomial of degree ( n- 1) relative to the variable t. At t
= t 1 ,
t 2 ,
…, t n polynomial values are the same as r(t 1),
r(t 2),
…, r(t n) respectively. The yield curve equation for the term structure obtained in Example 8.2 is:
[t 1 ,
t n]. Then r(t) is a polynomial of degree ( n- 1) relative to the variable t. At t
= t 1 ,
t 2 ,
…, t n polynomial values are the same as r(t 1),
r(t 2),
…, r(t n) respectively. The yield curve equation for the term structure obtained in Example 8.2 is:
r(t)
 0,00633
t 4
- 0,031 t 3
+ 0,04442 t 2
- 0,00325 t+ 0.0465, where t
0,00633
t 4
- 0,031 t 3
+ 0,04442 t 2
- 0,00325 t+ 0.0465, where t .
.
Using the obtained curve, we calculate the cost of a bond without credit risk, payments on which with respect to the moment t= 0 are specified in the table:
The market value of this bond at the time t= 0 is, according to (8.3):
P
=
 .
.
Approximate values of annual risk-free interest rates for investments for 0.7 years and 1.7 years are, respectively:
r(0,7)
 0,00633
0,00633 (0,7) 4
- 0,031
(0,7) 4
- 0,031 (0,7) 3
+ 0,04442
(0,7) 3
+ 0,04442 (0,7) 2
- 0,00325
(0,7) 2
- 0,00325 0,7
+ 0,0465 = 0,0569,
0,7
+ 0,0465 = 0,0569,
r(1,7)
 0,00633
0,00633 (1,7) 4
- 0,031
(1,7) 4
- 0,031 (1,7) 3
+ 0,04442
(1,7) 3
+ 0,04442 (1,7) 2
- 0,00325
(1,7) 2
- 0,00325 1,7
+ 0,0465 = 0,0699.
1,7
+ 0,0465 = 0,0699.
Then the market value of this bond
P
=
 =
112,14.
=
112,14.
The considered “bootstrapping procedure” for obtaining theoretical values of risk-free interest rates can be used if there are bonds on the market that are suitable for this procedure. Consider another method for obtaining theoretical values of interest rates.
Suppose we know the term structure of interest rates r(t 1), r(t 2), …, r(t k) for investments on t 1 , t 2 ,…, t k years, and there is a bond in the market with no credit risk worth P, through which t 1 , t 2 ,…,t k , t k + 1 , …, t n years promised payments With 1 , With 2 ,…,With k , With k +1 ,…,With n respectively. Approximate values of risk-free interest rates r(t k +1), r(t k +2), …, r(t n) can be found using linear interpolation on the segment [ t k , t n]. For this, it is assumed r(t n) = r. Risk free interest rate r(t k) is known. Then
 ,
,
 ,
,
……………….. (8.6)
 ,
,
r(t n) = r,
where t k
+ 1 ,
t k
+ 2 ,
…, t n –
1  [t k ,
t n ].
[t k ,
t n ].
Since the price of a bond P in the moment t= 0 is known, then
Substituting in this expression instead of r(t k + 1), r(t k + 2), …, r(t n) of equality (8.6), we obtain an equation with one unknown r. The solution of this equation is found by the method of linear interpolation. Knowing r, according to formulas (8.6) we find risk-free interest rates r(t k +1), r(t k + 2), …, r(t n). Thus, we have the term structure of interest rates r(t 1), r(t 2), …,r(t k), r(t k +1),…, r(t n) on t n– summer range relative to the moment t= 0.
Example 8.3. Using linear interpolation, construct the yield curve if annual risk-free interest rates are known:
r(0,5) = 0,06; r(1) = 0,07; r(1,5) = 0,08
and given a bond (without credit risk) with the following payment stream:
Equation (8.7) for this bond has the form:
We use linear interpolation on the segment . As r(1,5)
= 0,08, r(2,5)
= r, then r(2) 0,08
0,08 + r
+ r =
0,04 + 0,5r. Then it is enough to solve the equation
=
0,04 + 0,5r. Then it is enough to solve the equation
86,01581 =
 .
.
Solving this equation by linear interpolation, we find r
 0,10489.
0,10489.
Hence, r(2)
 0,04 + 0,5r
= 0,09245, r(2,5)
0,04 + 0,5r
= 0,09245, r(2,5) 0.10489. Thus, according to the given r(0,5)
= 0,06; r(1)
= 0,07; r(1.5) = 0.08 and calculated
0.10489. Thus, according to the given r(0,5)
= 0,06; r(1)
= 0,07; r(1.5) = 0.08 and calculated
r (2)
(2)
 0,092;
r(2,5)
0,092;
r(2,5) 0.105 values of risk-free interest rates, you can build a yield curve:
0.105 values of risk-free interest rates, you can build a yield curve:
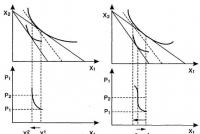
The yield curve obtained for bonds that do not have credit risk is also used to evaluate risky instruments in the market. Theoretical values of risk-free interest rates with the addition of a risk premium are used to value all types of bonds. In addition, the shape of the yield curve is seen as a reflection of the likely direction of future changes in interest rates. money market. On fig. 1.8.3 shows four main forms of the yield curve: 1 - normal (increasing) curve; 2 - reverse (decreasing) curve; 3 - "humped" curve; 4 – flat (horizontal) curve.

There are two main theories that explain the shape of yield curves - the theory of expectations and the theory of market segmentation. A rising curve most often means an expected increase in the inflation rate. A decreasing curve most often indicates an expected decline in the inflation rate. A horizontal yield curve means that the annual risk-free interest rates for investments are the same for all maturities. The horizontal curve is used in the study of some of the most important concepts in the theory of fixed income financial investments. For example, such as the duration and convexity of a bond, the cost of investing in a bond, the immunization of a bond portfolio.
| Option | №№ tasks | Option | №№ tasks | Option | №№ tasks |
| 1 | 1, 30, 31 | 6 | 6, 25, 36 | 11 | 11, 20, 41 |
| 2 | 2, 29, 32 | 7 | 7, 24, 37 | 12 | 12, 19, 42 |
| 3 | 3, 28, 33 | 8 | 8, 23, 38 | 13 | 13, 18, 43 |
| 4 | 4, 27, 34 | 9 | 9, 22, 39 | 14 | 14, 17, 44 |
| 5 | 5, 26, 35 | 10 | 10, 21, 40 | 15 | 15, 16, 45 |
Task 1. The nominal value of an ordinary bond N = 5000 rubles. Coupon rate c = 15%, remaining maturity of the bond n = 3 years, current market interest rate i = 18%. Determine the current market value of the bond.
Task 2. Determine the current value of a three-year bond with a face value of 1000 units. and an annual coupon rate of 8% paid quarterly if the rate of return (market rate) is 12%.
Task 3. Determine the current value of 100 units. par value of a bond with a maturity of 100 years, based on the required rate of return of 8.5%. The coupon rate is 7.72%, paid semi-annually. (The bond is perpetual).
Task 4. What price would an investor pay for a $1,000 zero coupon bond? and maturity in three years if the required rate of return is 4.4%.
Task 5. The bank bond has a face value of 100,000 units. and maturity in 3 years. The coupon rate on the bond is 20% per annum, accrued once a year. Determine the value of the bond if the investor's required yield is 25% and the coupon is accumulated and paid along with the face value at maturity.
Task 6. Perpetual bonds with a coupon of 6% of the face value and a face value of 200 den. should provide the investor with a yield of 12% per annum. What is the maximum price an investor will buy this financial instrument?
Task 7. You are a holder of a $5,000 bond that yields a fixed annual return of $100 for 5 years. The current interest rate is 9%. Calculate the current value of the bond.
Task 8. Estimate the market value of a municipal bond intended for public circulation, the par value of which is 100 rubles. The bond has 2 years to maturity. The nominal interest rate on the bond (used to calculate the annual coupon yield as a percentage of its face value) is 20%, the coupon yield is paid quarterly. The yield on comparable risks (also risk-free to hold and the same maturity) government bonds is 18%.
Task 9. Estimate the market value of a municipal bond intended for public circulation, the nominal value of which is 200 rubles. The bond has 3 years to maturity. The nominal interest rate on the bond (used to calculate the annual coupon yield as a percentage of its face value) is 15%. The yield on comparable risks (also risk-free to hold and the same maturity) government bonds is 17%.
Task 10. The company announces the issue of bonds with a par value of 1000 thousand rubles. with a coupon rate of 12% and a maturity of 16 years. At what price would these bonds sell in the efficient capital market if the required return to investors on bonds with a given level of risk is 10%?
Task 11. The firm issues bonds with a face value of 1000 thousand rubles, a coupon rate of 11%. The required return for investors is 12%. Calculate the current value of the bond with the maturity of the bond: a) 30 years; b) 15 years; c) 1 year.
Task 12. The nominal value of the bond is 1200 rubles, the maturity is 3 years, the coupon rate is 15%, the coupon is paid once a year. It is necessary to find the intrinsic value of the bond if the rate of return acceptable to the investor is 20% per annum.
Task 13. The face value of the bond is 1,500 rubles, the maturity is 3 years, the coupon rate is 12%, the coupon is paid twice a year. It is necessary to find the intrinsic value of the bond if the rate of return acceptable to the investor is 14% per annum.
Task 14. Terms of the bond issue: term 5 years, coupon yield - 8%, semi-annual payments. The expected average market yield is 10.5% per annum. determine the current price of the bond.
Task 15. There are two options for the terms of circulation of bonds. Coupon rates are equal to 8% and 12%, terms of 5 and 10 years. The expected market rate of return is 10%. Coupon income is accumulated and paid at the end of the circulation period together with the face value. Choose the cheapest option.
Bond yield
Task 16. There are two 3-year bonds. Bond D with an 11% coupon is sold at 91.00. Bond F with a 13% coupon is sold at par. Which bond do you prefer?
Task 17. Coupon 3-year bond A with a face value of 3 thousand rubles. sold at the rate of 0.925. Coupon payment is provided once a year in the amount of 360 rubles. Coupon 3-year bond B with a coupon of 13% is sold at par. Which bond do you prefer?
Task 18. The nominal value of a zero-coupon bond is 1,000 rubles. The current market value is 695 rubles. Repayment period 4 years. Deposit rate - 12%. Determine the feasibility of acquiring bonds.
Task 19. A bond with a par value of N = 1000 rubles. with a coupon rate c = 15% was purchased at the beginning of the year for 700 rubles. (for less than face value). After receiving the coupon payment at the end of the year, the bond was sold for 750 rubles. Determine the profitability of the operation for the year.
Task 20. A bond with a nominal value of 1000 rubles. with a coupon rate of 15% and a maturity of 10 years was purchased for 800 rubles. Determine the bond yield by interpolation.
Task 21. A bond with a nominal value of 1500 rubles. with a coupon rate of 12% (semi-annual accrual) and a maturity of 7 years was purchased for 1000 rubles. Determine the bond yield by interpolation.
Task 22. A perpetual bond yielding a 20% coupon rate was purchased at a rate of 95. Determine the financial efficiency of the investment, provided that interest is paid: a) once a year, and b) quarterly.
Task 23. The corporation issued zero-coupon bonds maturing in 5 years. Selling rate - 45. Determine the yield of the bond at the maturity date.
Task 24. A bond yielding 10% per annum relative to face value was purchased at a rate of 60, with a maturity of 2 years. Determine the total return to the investor if the face value and interest are paid at the end of the circulation period.
Task 25. A zero-coupon bond with a maturity of 10 years was issued. The bond rate is 60. Find the total yield at the maturity date.
Task 26. A bond with an income of 15% per annum of face value, a rate of 80, a maturity of 5 years. Find the total yield if the par and interest are paid at the end of the maturity.
Task 27. A bond with a maturity of 6 years with an interest rate of 10% was purchased at a rate of 95. Find the total yield by interpolation.
Task 28. The current market rate of the bond is 1200 rubles, the face value of the bond is 1200 rubles, the maturity is 3 years, the coupon rate is 15%, the coupon payments are annual. Determine the total yield of a bond using the average method and the interpolation method.
Task 29. A five-year bond that pays annual interest at 8% is bought at a rate of 65. Determine the current and total yields.
Task 30. Coupon 5-year bond W with a face value of 10 thousand rubles. sold at the rate of 89.5. Coupon payment is provided once a year in the amount of 900 rubles. Coupon 6-year bond V with an 11% coupon is sold at par. Which bond do you prefer?
Bond Risk Assessment
Task 31. The possibility of acquiring the OJSC's bonds, the current quotation of which is 84.1, is being considered. The bond has a maturity of 6 years and a coupon rate of 10% per annum, paid semi-annually. The market rate of return is 12%.
c) How will the information that the market rate of return has risen to 14% affect your decision?
Task 32. The OJSC issued 5-year bonds with a coupon rate of 9% per annum, paid every six months. At the same time, 10-year bonds of OJSC with exactly the same characteristics were issued. The market rate at the time of issuance of both bonds was 12%.
Task 33. The OJSC issued 6-year bonds with a coupon rate of 10% per annum, paid semi-annually. At the same time, 10-year bonds of the JSC were issued with a coupon rate of 8% per annum, paid once a year. The market rate at the time of issuance of both bonds was 14%.
a) At what price were the corporate bonds placed?
b) Determine the durations of both bonds.
Task 34. The possibility of purchasing Eurobonds of the JSC is being considered. Release date - 06/16/2008. The maturity date is 06/16/2018. Coupon rate - 10%. Number of payments - 2 times a year. The required rate of return (market rate) is 12% per annum. Today is 12/16/2012. The average course price of the bond is 102.70.
b) How will the price of the bond change if the market rate: a) increases by 1.75%; b) will fall by 0.5%.
Task 35. The initial price of a 5-year bond is 100 thousand rubles, the coupon rate is 8% per annum (paid quarterly), the yield is 12%. How will the price of a bond change if the yield increases to 13%.
Task 36. You have to pay back $200,000 in three years from your bond portfolio. The duration of this payment is 3 years. Suppose you can invest in two types of bonds:
1) zero-coupon bonds with a maturity of 2 years (current rate - 857.3 dollars, face value - 1000 dollars, placement rate - 8%);
2) bonds with a maturity of 4 years (coupon rate - 10%, face value - $1,000, current rate - $1,066.2, placement rate - 8%).
Problem 37. The possibility of acquiring the OJSC's bonds, the current quotation of which is 75.9, is being considered. The bond has a maturity of 5 years and a coupon rate of 11% per annum, paid semi-annually. The market rate of return is 14.5%.
a) Is buying a bond a profitable transaction for an investor?
b) Determine the duration of the bond.
c) How will the information that the market rate of return has fallen to 14% affect your decision?
Problem 38. The OJSC issued 4-year bonds with a coupon rate of 8% per annum, paid quarterly. At the same time, 8-year bonds of the JSC were issued with a coupon rate of 9% per annum, paid every six months. The market rate at the time of issuance of both bonds was 10%.
a) At what price were the corporate bonds placed?
b) Determine the durations of both bonds.
c) Shortly after the issue, the market rate rose to 14%. Which bond will change the most?
Task 39. The OJSC issued 5-year bonds with a coupon rate of 7.5% per annum, paid quarterly. At the same time, 7-year bonds of the OJSC were issued with a coupon rate of 8% per annum, paid every six months. The market rate at the time of issuance of both bonds was 12.5%.
a) At what price were the corporate bonds placed?
b) Determine the durations of both bonds.
c) Shortly after the issue, the market rate fell to 12%. Which bond will change the most?
Task 40. The possibility of acquiring bonds of the JSC is being considered. Release date - 20.01.2007. The maturity date is 01/20/2020. Coupon rate - 5.5%. Number of payments - 2 times a year. The required rate of return (market rate) is 9.5% per annum. Today is 01/20/2013. The average course price of the bond is 65.5.
a) Determine the duration of this bond at the date of the transaction.
b) How will the price of the bond change if the market rate: a) increases by 2.5%; b) will fall by 1.75%.
Task 41. The face value of a 16-year bond is 100 rubles, the coupon rate is 6.2% per annum (paid once a year), the yield is 9.75%. How will the price of a bond change if the yield increases to 12.5%. Perform analysis using duration and convexity.
Task 42. You need to pay back $50,000 in three years from your bond portfolio. The duration of this payment is 5 years. There are two types of bonds available on the market:
1) zero-coupon bonds with a maturity of 3 years (current rate - $40, face value - $50, placement rate - 12%);
2) bonds with a maturity of 7 years (coupon rate - 4.5%, coupon income is paid every six months, face value - $50, current rate - $45, placement rate - 12%).
Build an immunized bond portfolio. Determine total cost and the number of bonds purchased.
Task 43. The face value of a 10-year bond is 5,000 rubles, the coupon rate is 5.3% per annum (paid once a year), the yield is 10.33%. How will the price of a bond change if the yield increases to 11.83%. Perform analysis using duration and convexity.
Task 44. The possibility of acquiring the OJSC's bonds, the current quotation of which is 65.15, is being considered. The bond has a maturity of 5 years and a coupon rate of 4.5% per annum, paid quarterly. The market rate of return is 9.75%.
a) Is buying a bond a profitable transaction for an investor?
b) Determine the duration of the bond.
c) How will the information that the market rate of return has increased to 12.25% affect your decision?
Task 45. You have to pay back $100,000 in three years from your bond portfolio. The duration of this payment is 4 years. There are two types of bonds available on the market:
1) zero-coupon bonds with a maturity of 2.5 years (current rate - $75, face value - $100, placement rate - 10%);
2) bonds with a maturity of 6 years (coupon rate - 6.5%, coupon income is paid quarterly, face value - $100, current rate - $85, placement rate - 10%).
Build an immunized bond portfolio. Determine the total cost and number of bonds to be purchased.
1. Anshin V.M. Investment analysis. - M.: Delo, 2002.
2. Galanov V.A. Securities market: textbook. - M.: INFRA-M, 2007.
3. Kovalev V.V. Introduction to financial management. - M.: Finance and statistics, 2007
4. Handbook of the financier in formulas and examples / A.L. Zorin, E.A. Zorin; Ed. E.N. Ivanova, O.S. Ilyushina. - M.: Professional publishing house, 2007.
5. Financial mathematics: mathematical modeling financial transactions: studies. allowance / Ed. V.A. Polovnikova and A.I. Pilipenko. - M.: Vuzovsky textbook, 2004.
6. Chetyrkin E.M. Bonds: theory and yield tables. - M.: Delo, 2005.
7. Chetyrkin E.M. financial mathematics. – M.: Delo, 2011.
11.2. Measuring Bond Yields
Bond yield. The yield of bonds is characterized by several indicators. Distinguish coupon(coupon rate) tech at schuyu(current, running yield) and full return(yield to maturity, redemption yield, yield).
The coupon yield is determined when the bond is issued and therefore does not need to be calculated. Current yield characterizes the ratio of coupon income to the purchase price of a bond. This parameter does not take into account the second source of income - receiving the face value or redemption price at the end of the term. Therefore, it is unsuitable when comparing the yield of different types of bonds. Suffice it to say that zero-coupon bonds have a current yield of zero. At the same time, they can be very profitable, given the entire period of their "life".
The most informative indicator is the total return, which takes into account both sources of income. It is this indicator that is suitable for comparing the return on investment in bonds and other securities. So total return, or to use the old commercial terminology, room rate, measures the real performance of an investment in a bond for an investor as an annual compound interest rate. In other words, the accrual of interest at the rate of placement on the purchase price of the bond fully ensures the payment of coupon income and the amount to redeem the bond at the end of the term.
Let us consider the methodology for determining the yield indicators of various types of bonds in the sequence adopted above when classifying bonds according to the method of paying income.
Bonds without mandatory redemption with periodic interest payments. Although this type of bond is extremely rare, familiarity with them is necessary to fully understand the methodology for measuring yield. When analyzing this type of bonds, we do not take into account the payment of par value in the indefinite future.
Let us introduce the following notation:
g - declared rate of annual income (coupon interest rate);
i t - current profitability;
i- total yield (room rate).
The current yield is as follows:
i t = 100. (11.2)
If coupons are paid R once a year (each time at the rate g/ p), then in this case, formula (11.2) is applied in practice, although the summation of income paid at different points in time, strictly speaking, is incorrect.
Since the coupon income is constant, the current yield of the bonds sold changes along with the change in their market price. For a bondholder who has already invested some money, this value is constant.
Let's move on to total return. Since coupon income is the only source of current income, it is obvious that the total yield of the bonds in question is equal to the current one in the case when coupon payments are annual: i = i t. If interest is paid R once a year (each time according to the norm g / p), then according to (2.8) we obtain
![]() (11.3)
(11.3)
Example 11.1. An annuity that brings 4.5% of income, bought at a rate of 90. What is the financial efficiency of the investment, provided that interest is paid once a year, quarterly ( p = 4)?
i = i t = 100 = 0,05; i = - 1 = 0,0509.
Bonds without paying interest. This type of bond provides its owner with the difference between the face value and the purchase price as income. The rate of such a bond is always less than 100. For
to determine the rate of the premises, we equate the present value of the face value to the purchase price:
Nv n = P, or v n = ,
where n - the term until the redemption of the bond. After which we get
Example 11.2. Corporation X issued zero-coupon bonds maturing in five years. Realization rate - 45. Yield of the bond at the maturity date

those. the bond provides the investor with 17.316% of annual income.
Bonds with payment of interest and face value at the end of the term. Interest here is accrued for the entire term and is paid in one amount (lump sum) along with the face value. No coupon income. Therefore, the current yield can be conditionally considered zero, since the corresponding interest is received at the end of the term.
Find the total return by equating the present value of income to the price of the bond:
(1 + g)nNv n = P, or .
It follows from the last formula that
If the bond price is less than 100, then i > g.
Example 11.3. A bond yielding 10% per annum relative to face value was purchased at a rate of 65, with a maturity of three years. If the face value and interest are paid at the end of the term, then the total return for the investor will be
i = - 1 = 0.26956, or 26.956%.
Bonds with periodic interest payments and redemption of the face value at the end of the term. This type of bonds has received the greatest distribution in modern practice. For such a bond, you can get all three yield indicators - coupon, current and full. The current yield is calculated according to the above formula (11.2). As for the total yield, to determine it, it is necessary to equate the present value of all receipts to the price of the bond. The discounted nominal value is equal to Nv n. Since coupon receipts are a constant postnumerando annuity, the annuity term is equal to gN, and its present value is gNa n ; i (if coupons are paid annually) and if these payments are made R once a year (each time at the rate g/ p). As a result, we get the following equalities:
for bonds with annual coupons
![]() (11.6)
(11.6)
Divided by N, we find
![]() (11.7)
(11.7)
for a bond with coupon redemption by semi-annual and quarterly, we obtain
![]() (11.8)
(11.8)
where is the reduction factor p- urgent rent ( p = 2, p = 4).
In all the above formulas v n means the discount multiplier at the unknown annual rate of the premises i.
In foreign practice, however, for bonds with semi-annual and quarterly current income payments, the annual nominal room rate is used for discounting, and the number of discounting times per year is usually taken equal to the number of coupon income payments. Thus, the initial equality for calculating the room rate has the form
where i - nominal annual rate;
rp - the total number of coupon payments; g - annual percentage of payments on coupons.
When solving the above equalities for an unknown quantity i face the same problems as in the calculation i by a given value of the annuity reduction coefficient - see paragraph 4.5. The desired values of the room rate are calculated either by interpolation or by some iterative method.
Let's estimate i using linear interpolation:
![]() (11.10)
(11.10)
where i" and i" - the lower and upper values of the premise rate, limiting the interval within which the unknown rate value is expected to lie;
K" , K" - calculated values of the exchange rate, respectively, for rates i" , i" . The interval of rates for interpolation is determined taking into account the fact that i > g at K < 100.
It is also possible to apply the method of approximate estimation, according to which
 . (11.11)
. (11.11)
In this formula, the average annual income from the bond is correlated with its average price. For the simplicity of the calculation, however, one has to pay for the loss of the accuracy of the estimate.
Example 11.4. A bond with a term of five years, on which interest is paid once a year at a rate of 8%, was purchased at a rate of 97.
Bond current yield 8 / 97 = 0,08247.
To estimate the total return, we write the original equation (11.7):
0,97 = (1 + i) -5 + 0,08a 5; i.
For interpolation, we will take the following values of rates: i" = 0,085, i" = 0.095. According to (11.7) we find
1,085 -5 + 0,08a 5;8,5 = 98,03;
= 1,095 -5 + 0,095a 5;9,5 = 94,24.
i = 8,5 + (9,5 - 8,5) = 8,77.
For verification, we calculate the exchange rate for the premises rate of 8.77%. Get
= 1,0877 -5 + 0,08a 5;8,77 = 96,99.
As you can see, the settlement rate is very close to the market rate - 97. The approximate solution according to (11.11) gives
i
= ![]() = 8,73,
= 8,73,
which corresponds to the market rate of 97.2. The error is higher than when using linear interpolation.
Bonds with a redemption price that differs from par. In this case, interest is charged on the nominal amount, and the capital gain is equal to S - R, where With- redemption price. Accordingly, when assessing the rate of the premises, it is necessary to make appropriate adjustments.
tives in the above formulas. For example, by making adjustments to (11.6) and (11.7), we obtain
and instead of (11.11)
 (11.14)
(11.14)
Example 11.5. Let's compare the yield of two bonds with annual interest payments (Table 11.1). Bond Options A taken from the previous example.
Table 11.1
Yields for these bonds are given in Table. 11.2.
Table 11.2
As you can see, in terms of total return, the advantage is on the side of the bond A, although its current yield is lower than that of the second. The approximate calculation method according to (11.11) - the corresponding indicators are given in brackets - noticeably overestimated the estimate of the bond's total return B.
All of the formulas discussed above for calculating the total yield assume that the valuation is made at the beginning of the bond's term or at the date of payment of interest. For the case where the valuation is made between two interest payment dates, the above formulas will give biased valuations.
M.: Delo, 2004. - 280 p.
ISBN 5-7749-0200-5
Download(direct link) :
invest-analyz.djvu Previous 1 .. 31 > .. >> Next
Current yield - the ratio of coupon income to the purchase price.
Yield to maturity takes into account coupon yield and redemption yield (sometimes called the premise rate).
Yield by types of bonds. /. Bonds without mandatory redemption with periodic interest payments. If c is the coupon rate, rt is the current yield, then
r, \u003d Ms / P \u003d c 100 / K. (9.1)
2. Bonds without paying interest. Yield is formed as the difference between the face value and the purchase price. The price of this bond is less than 100.
The balance of the operation will be written as follows: P = M(I + r)~", where n is the maturity of the bond, r is the total yield of the bond, (1 + r)~n = A/100;
g "1 / 4JK / 100 - 1. (9 2)
EXAMPLE. A zero-coupon bond with a maturity of 10 years was issued. Bond rate - 60. Find the total yield on the maturity date.
Solution, r = 1 / (^60/100) -1 - 0.052, or 5.2%.
3. Bonds with payment of interest and face value at the end of the term (reinvestment of coupon income). Operation balance: M (1 + c)n (1 + r)~n = P or [(1 + c)/(1 + r)]" = /r/100;
r"(1+s)/^AG/100-1. (9 3)
EXAMPLE. Bonds with an income of 15% per annum of face value, a rate of 80, a maturity of 5 years. Find the total yield if the face value and interest are paid at the end of the term.
Solution, r = (1 + 0.15) / ^ / 80/100 -1 = 0.202, or 20.2%.
4. Bonds with periodic interest payments and par value redemption at the end of the term. Operation balance:
CM CM CM M
1 + r (1 + r)2 (1 + r)" (1 + r)"
P \u003d M (I + r) "n + cM ^j (I + r)"", where / is the period from the purchase of bonds to the payment of coupon income.
The determination of the unknown value of the total return can be made by three methods: the so-called approximate method, the method of linear extrapolation and the trial and error method.
For the approximate method, the formula is used
CM + (M - P)In
(M+P)? KU"
c + (1 -Yu / p G-- (1-L) / 2 (96)
To use the linear interpolation method (description of the method is given in Section 3.6), we divide both parts of formula (9.4) by M:
A / 100 \u003d (1 + r) - "+ cV, (9.7)
where ar is the coefficient of reduction of rent at the rate r for the period n.
The total return r can be found by linear interpolation:
where н and гв - the lower and upper limits of the total profitability; Kn and K3 - the lower and upper limits of the course calculated for h and g according to the formula (9.7); Kv< К < Кн.
It should be noted that as the yield increases, the price of the bond decreases.
EXAMPLE. A bond with a maturity of 6 years with an interest rate of 10% was bought at a rate of 95. Find the total yield.
Decision. To determine the coefficients of reduction of rent аг, we use the already known formula (3.20).
Let's put rI = 10%, /"v = 15%. Then:
KJlOO \u003d 1.10 "6 + 0.1<76;IO = 0,564 + 0,1 4,355 = 0, 99;
Kjm \u003d 1.15 "6 + 0.1 i6: 15 \u003d 0.432 + 0.1 3.784 \u003d 0.81;
/*= 0,10 + [(0,99 - 0,95)/(0,99 - 0,81)] (0,15 - 0,10) = 0,11.
Check: 1.11 "6 + 0.1 a.i = 0.535 + 0.1 4.23 = 0.958.
The trial and error method consists in choosing the value of r in such a way that the equality (9.4) (or (9.7)) turns out to be true.
Duration is one of the indicators of bond volatility. This term is a tracing paper from the English duration, which translates as "duration". This indicator was first studied by Frederick Macaulay in 1938. He defined this indicator as the weighted average maturity of the cash flow of a security1. Macaulay duration is calculated using the formula:
where t is the maturity or cash flow element of the bond; CF1 is the value of the bond cash flow element in the year /; r - yield to maturity (full yield).
The Macaulay duration index, calculated by formula (9.9), is measured in years.
Special attention should be paid to the fact that discounting is carried out at the rate of return to maturity, which must first be determined, for which the methods discussed above can be used. In addition, we note that the denominator of the formula for calculating duration is the price of a bond, since
For bonds for which coupon income is paid m times a year, the calculation formula takes the form:
9.4. Duration
(average duration of payments)
2 CF1(I + gG<
¦2 CZ)(I + g/tG
The Handbook of Fixed Income Securities. P. 85.
EXAMPLE. A bond with a maturity of 6 years, coupon rate - 10%, face value - $100. Yield to maturity - 11%.
Table 9.2
1
(1+r)""
CF1
CF1(X + g)""
tCFt(\+r)-"
I
0,9009
10
9,009
9,009
2
0,8116
10
8,P6
16,232
3
0,7312
10
7,312
21,936
4
0,6587
10
6,587
26,348
5
0,5935
10
5,935
29,675
6
0,5346
on
58,806
352,836
95,765
451,4272
We get:
D = 451.4272/95.765 = 4.7 years.
Duration can also be viewed as the elasticity of the price of a bond to a change in the interest rate (more precisely, the value of 1 + r). In general terms, the elasticity coefficient is the ratio of the relative increase in one indicator to the relative increase in another indicator. In this case, these indicators are the price of the bond and the interest rate.